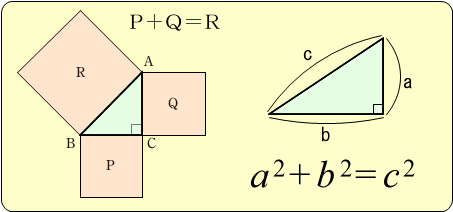
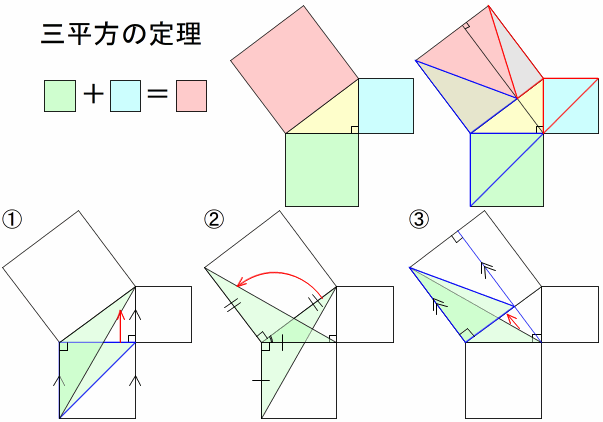
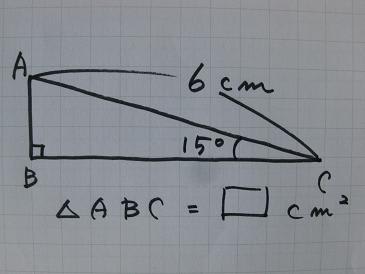
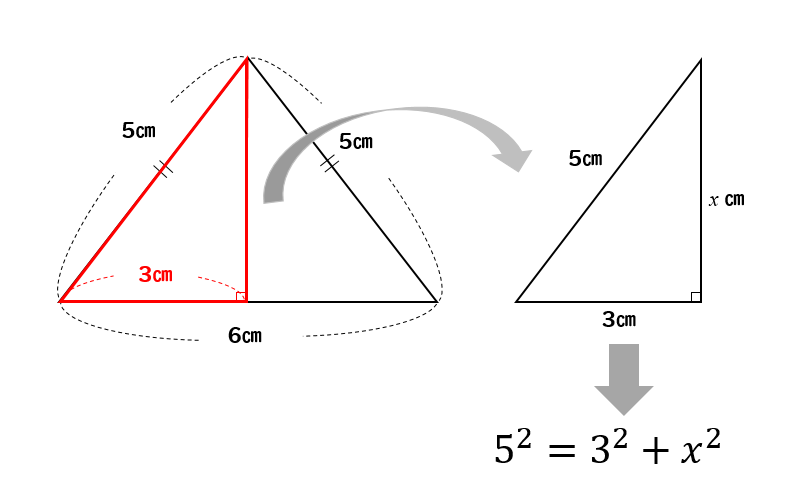
三平方の定理の証明5選直角三角形や正方形を重ねましょう 三平方の定理 (別名ピタゴラスの定理)とは、底辺が a a 、高さが b b 、斜辺が c c である直角三角形において、 a 2 b 2 = c 2 a 2 b 2 = c 2 が成り立つことでしたね。 この式を証明するポイントを1 三平方の定理の内容:直角三角形と辺の長さの関係 11 分からない辺の長さを計算できる三平方の定理 12 ピタゴラスの定理が成り立つ証明 2 特殊な形の三角形で利用される三平方の定理 21 直角二等辺三角形:角度が45°の直角三角形 22 角度が30°と60 三平方の定理を使って面積を求める方法は? 問題を使って解説するよ! 次の三角形の面積を求めましょう。 まず、底辺を6㎝とした場合の高さとなるような線を引きます。 すると、三角形が2つの直角三角形に分けることができますね。 そこから左に

三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ
直角三角形 面積 三平方の定理
直角三角形 面積 三平方の定理- 三平方の定理(ピタゴラスの定理) 上のような直角三角形で、次の等式が成り立つ。 a2 b2 = c2 a 2 b 2 = c 2 直角三角形の2辺がわかれば、残りの1辺も求まるというもので、紀元前から測量等でも使われてきました。 日本では中学3年生(義務教育! )で下の三平方の定理の証明の方法について,太郎さんと花子さんが考えています。あとの(1), (2)の各問いに答えなさい。 三平方の定理 直角三角形の直角をはさむ2辺の長さを a,b, 斜辺の長さをc とすると,次の関係が成り立つ。 a 2+ b = c




中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su
直角二等辺三角形の底辺と高さの長さは同じです。 底辺(高さ)の長さを「1」として、三平方の定理に代入すると「斜辺 2 =底辺 2 高さ 2 ⇒ 斜辺 2 =11=2 ⇒ 斜辺=√2」になります。 よって、直角二等辺三角形の辺の比は「1:1;√2」です。直角三角形abcが与えられたとき、斜辺bcを1辺とする正方形の面積は、他の2辺ab、acを1辺とする二つの正方形の面積の和に等しい。 すなわち、 bc 2 =ab 2 +ac 2 が成立する。 これを三平方の定理という。紀元前540年ごろギリシアの数学者ピタゴラスが発見したものといわれ、ピタゴラスの定理とし 解き方 直角三角形に対し三平方の定理を使います。 (2)は直角三角形が無いですね。 補助線を引いて直角三角形を作ります。 そのうえで高さを求めていきます。 解説 (1)次の三角形のabの長さを求めなさい。
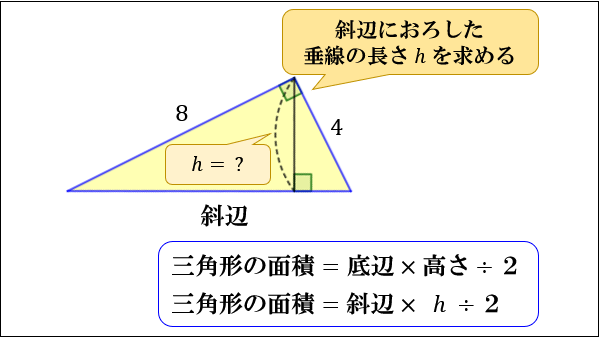
直角三角形の辺の比の3つのパターン 直角三角形の比は3つ覚えればいい?? こんにちは!ぺーたーだよ。 三平方の定理で覚えておきたいのは、 直角三角形の比 だよ。 これを覚えておけば、 三平方の定理を使わなくて辺の長さを計算できちゃうんだ。三辺から三角形の面積を求める 例題 ABCの面積を求める。 A B C 25cm 28cm 17cm 頂点Aから辺BCに垂線ADを引いて直角三角形を2つ作る。 A B C 25cm 28cm 17cm xcm (28x)cm D BD = xcm とすると DC = (28x)cm となる。 ABDで三平方の定理より AD2x2=252 → AD2= 252 x2 三平方の定理で直角三角形の辺の長さを計算してみると、 x² = 3² 5² x = √34 になるね。 答えが整数じゃなくてスッキリしないけど、こういう答えもありだ。 Step3 ピタゴラスが悩んだ直角二等辺三角形 つぎは、 直角二等辺三角形の辺の長さ を三平方
三平方の定理の公式を紹介します。下の図のように直角三角形の直角を挟む2辺をa,bとし、斜辺をcとすると a²b²=c² の等式が成立することを三平方の定理と言います。 三平方の定理の証明 三平方の定理の証明について紹介したいと思います。 3:4:5の三角形で,本当に直角ができるのでしょうか。 三角形の辺の長さの比と角の大きさには,どんな関係があるのでしょうか。 3:4:5は,斜辺の対角が直角です。このことは,三平方の定理として知られています。 3:4:5三平方の定理 例題 三平方の定理 三平方の定理2 三平方_平行四辺形の対角線 特別な直角三角形_補助線が必要な問題 二等辺三角形の面積 台形の面積 三平方_三辺の長さから三角形の面積を求める 三平方_座標平面の三角形 三平方_座標(最短距離) 三平方_座標(点と直線の距離) 三平方_折り返し




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
三平方の定理から, 辺の長さが整数である直角三角形を見つけることは, \(a^2b^2=c^2\) を満たすような整数 \((a, b, c)\) の組を見つけることと同じになります定理 直角三角形で、斜辺を直径とする半円が内接していて他の2辺を直径とする半円は外接している。 斜辺でない方の2辺の半円と直角三角形の和と斜辺の半円の面積の差は、元の直角三角形の面積と等しい。 つまり図では青と赤の面積が等しい。 直角二等辺三角形の辺の比は、必ず「 \color {red} {1 1 \sqrt {2}} 」 となります。 1 辺の長さからほかの辺の長さを簡単に求められるので、この比は必ず覚えておきましょう。 なぜこの比が成り立つかは、 三平方の定理 から示すことができます。 三平方の




三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題



見えますか タイルの模様からピタゴラスの定理 Note Board
重要 三平方の定理 直角三角形の直角をはさむ2辺の長さを a,b とし、斜辺の長さを c とすると、次の関係が成り立つ。 c 2 = a 2 b 2 {\displaystyle c^ {2}=a^ {2}b^ {2}} この定理を証明したのは古代ギリシアの数学者ピタゴラスであるとも言われているので、この三平方の定理は、直角三角形の3つの辺の長さの関係を表わした定理で、直角三角形の直角を挟む2つの辺の長さをそれぞれ a a 、 b b とし、斜辺の長さを c c とすると、 a2 b2 = c2 a 2 b 2 = c 2 の関係が成り立つ、という定理です。 それで、三平方の定理を使えば、 2× 2 =√3×√3+ 1 × 1 になることは納得できます。 そのため、次の内容は正しいことになります。 3 つの辺が√3と 2 と 1 の三角形は直角三角形になり、内側の角度は 90 度、 60 度、 30 度になる このことは三平方の定理




簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



直角三角形の辺の長さ 合同条件 面積について アタリマエ
三平方の定理を使えば,直角三角形の2辺の長さが分かれば残りの1辺の長さが求められる. たとえば右図では, b , c が分かっていれば a が求められる.直角三角形 110 /2件 表示件数 5 10 30 50 100 0 1 1245 60歳以上 / その他 / 非常に役に立った / 中3で学習する「三平方の定理」の中でも、これは応用問題です。例えば、こんな問題です。問題 上の図で、AB=、BC=21、CA=13です。 ABCの面積を求めなさい。まずは、三平方の定理までしか学習していない中3として、この問題をどう解くか考えてみま,セギ英数教室 角木優子




高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ




Mathematics 三平方の定理 3 いろいろな三角形 働きアリ
例 (1) 1 2 x 斜辺がxなので 1222=x2 x2 = 5 x > 0 より x= 5 (2) x 12 13 斜辺が13なので x2122直角三角形の各辺の長さの関係はピタゴラスの定理(三平方の定理)と呼ばれる。 記号⊿を使ってあらわすことがある。 直角三角形の直角以外の2つの角を、直角三角形の鋭角 と呼ぶ。それらの大きさの和は、直角に等しい。 三平方の定理とは、次のような定理です。 三平方の定理(ピタゴラスの定理) 上のような直角三角形で、次の等式が成り立つ。 a2 b2 = c2 a 2 b 2 = c 2 直角三角形の2辺がわかれば、残りの1辺も求まるというもので、紀元前から測量等でも使われてきました



円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト



感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社
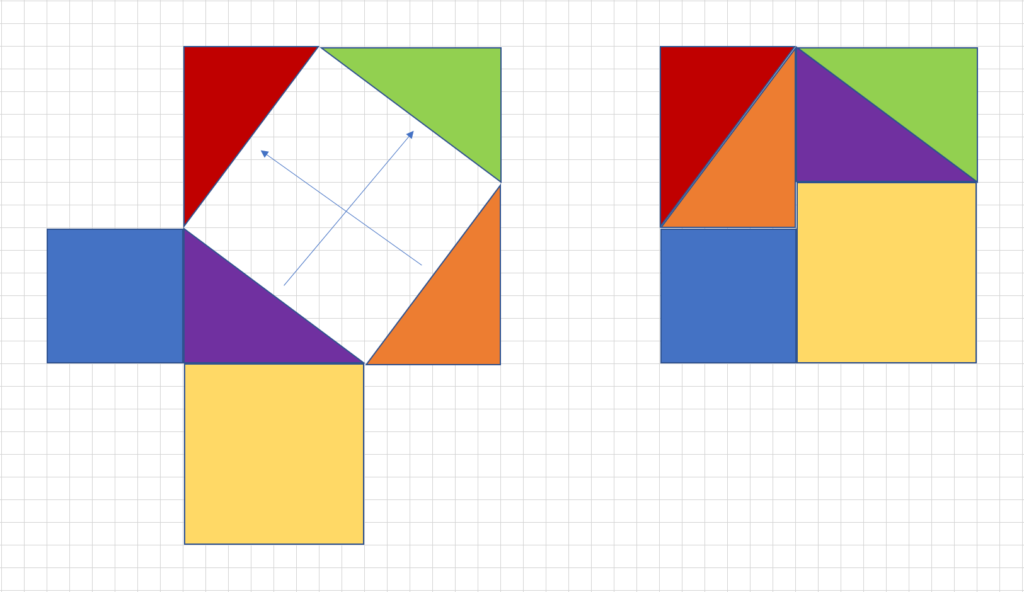
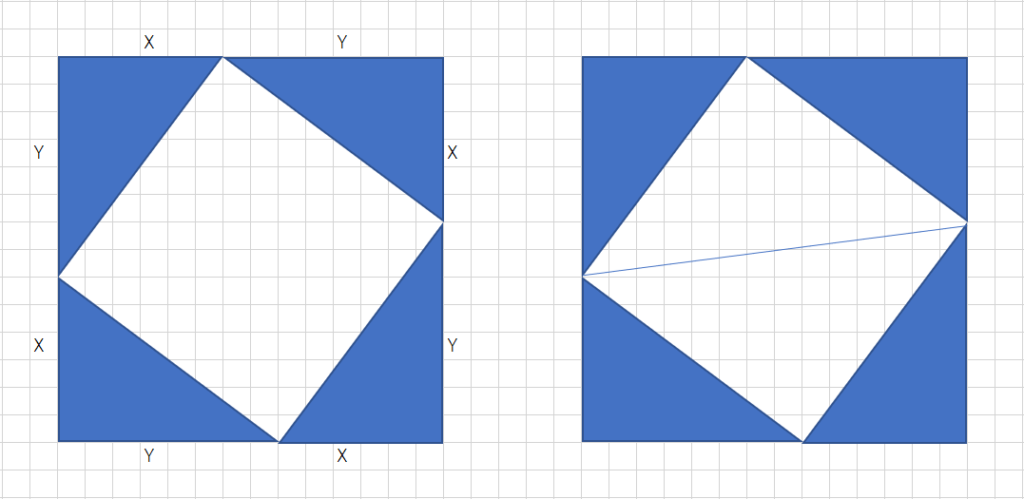
です。これは直角二等辺三角形の場合の三平方の定理ですね! やはり、ピタゴラスは只者ではありません。 ちなみに、上のタイルを一般の直角三角形に応用した図は です。ここで面積が 大きな正方形=小さな正方形+直角三角形×4三平方の定理を使うと、直角三角形の 2 つの辺の長さからもう一つの辺の長さを求めることができます。 このページでは、三平方の定理を分かりやすく説明しています。中学校で学習する前の人にも、三平方の定理の意味を理解してもらえるような解説にしているので、ぜひお読みください。 1.どんな定理か理解しよう! 三平方の定理はピタゴラスの定理、 勾股弦 こうこげん の定理とも呼びます。 この定理は、直角三角形の3つの辺の長さの関係を表しています。 上図の直角三角形では、直角を挟む2つの辺の長さがa、bで、斜辺の長さがcとなっています。




三平方の定理の拡張について考えよう 理科好き子供の広場



三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
三平方の定理 より 「底辺 a 、斜辺 c の直角三角形」の高さは b = √c2 − a2 「底辺 a の正三角形」の高さは h = √a2 − (a / 2)2 = √3 2 a ③ 2辺とその間の角の大きさを使った公式 三平方の定理が成り立つ整数の組 三平方の定理は、平方が登場してくる関係上どうしてもルートが出てきやすくなってしまいます。 そのため、辺の長さが整数の比になる直角三角形は、小さい数字の範囲内ではそれほど多くありません。 もちろん数字を 直角三角形 直角三角形の概要 ナビゲーションに移動検索に移動 直角三角形直角三角形の各辺の長さの関係はピタゴラスの定理(三平方の定理)と呼ばれる。記号⊿を使ってあらわすことがある。直角三角形の直角以外の2つの角を、直角三角形の鋭角



数学切り抜き帳




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット
藤原,第一巻 1, 222‐3頁 によれば,「勾股弦の定理」 (三平方の定理) を法則として明 示したのは,今村知商『竪亥録』 2, 109頁及び3, 50頁 が最初である勾股弦とは直 角三角形を指すが,和算では次図のように置き,勾は直角を挟む縦線,股は横線,弦は斜 93二等辺三角形の高さの求め方 まとめ 二等辺三角形の高さを求めるためには まず、頂角からまっすぐな線を引きましょう! すると、直角三角形を作ることができるので そこから三平方の定理を使ったり 角度がわかる場合には比を取って 高さを求めてき三平方の定理とは、直角三角形の3辺の長さの関係を表す公式の事を言います。 また、別名「ピタゴラスの定理」とも呼ばれています。 この呼び方の方が有名でしょうか。 古代中国でもこの定理は使われていて、それが日本に伝わり、江戸時代には鉤股弦




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube



3 4 5の三角形で 本当に直角ができる Note Board
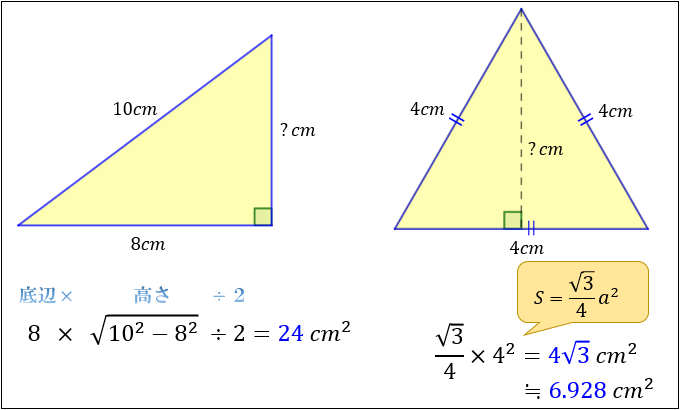
正三角形の高さと面積の求め方 について解説していくよ! ここでは、中3で学習する三平方の定理という知識を利用していきます。 三平方の定理があいまいな方は、まずはこちらの記事で確認しておいてくださいね(^^)三平方の定理 平面図形での活用(2) 1 半径10㎝の円の中心から、6㎝の距離に ある弦の長さを求めなさい。 378 10㎝ 6㎝ 円の中心Oから弦ABに垂線OHをひくと OAHは直角三角形だから、 AH=x ㎝とすると、三平方の定理より x +6 =10 x =




三平方の定理の証明と使い方




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく




中学受験算数 等積変形の利用 ヒポクラテスの月




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ
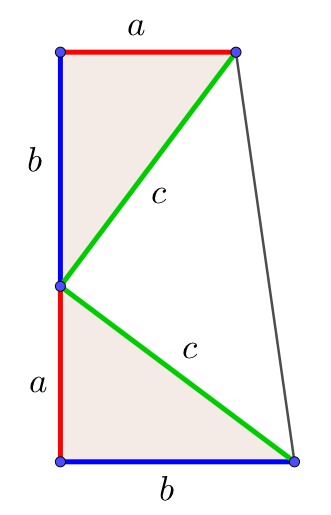



三平方の定理の証明3 大統領の台形 キソカラ




三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト




数学 中3 61 三平方の定理 基本編 Youtube




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社



三平方の定理



三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ



マッキーの教室 中2生徒の 三平方の定理 問題の質問に答える マッキーのつれづれ日記




中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog




三平方の定理の証明と使い方




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月




中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su




高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ




三平方の定理と二等辺三角形 Youtube




知っていて当たり前 三平方の定理の応用 名寄 算数数学教室より



三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典




無料 中3数学 発展 応用問題 問題プリント 333 三平方の定理1




三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ




三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト




三平方の定理で辺を求める Youtube



中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



1




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット



中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog



三平方の定理の導入 Geogebra




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




正方形を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト




カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 1 4



高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ



平面の変換




三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




中学数学 三平方の定理
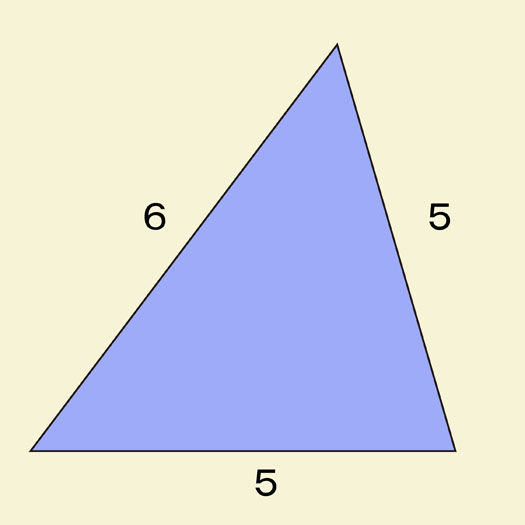



この三角形の面積を超簡単に解く方法が凄い 秒刊sunday



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学



受験数学かずスクール 三平方の定理の公式の証明の仕方



三平方の定理




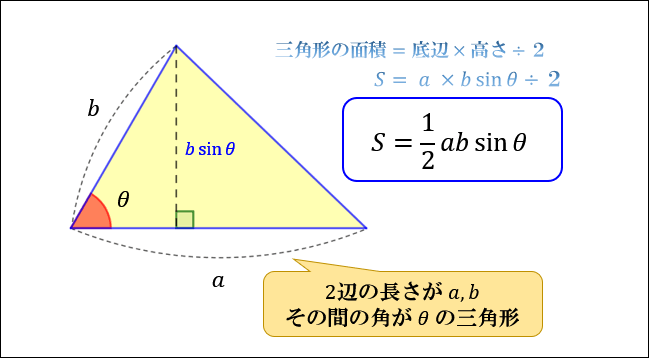
高校数学 三角比による三角形の面積の公式 S 1 2bcsina の証明と利用 受験の月



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典



ピタゴラスの定理とその証明




三平方の定理の証明と使い方




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく




高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




三角定規の直角三角形のときは 比の計算で簡単に求めよう 中学や高校の数学の計算問題



中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ



中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog




直角三角形の辺の長さ 合同条件 面積について アタリマエ



1
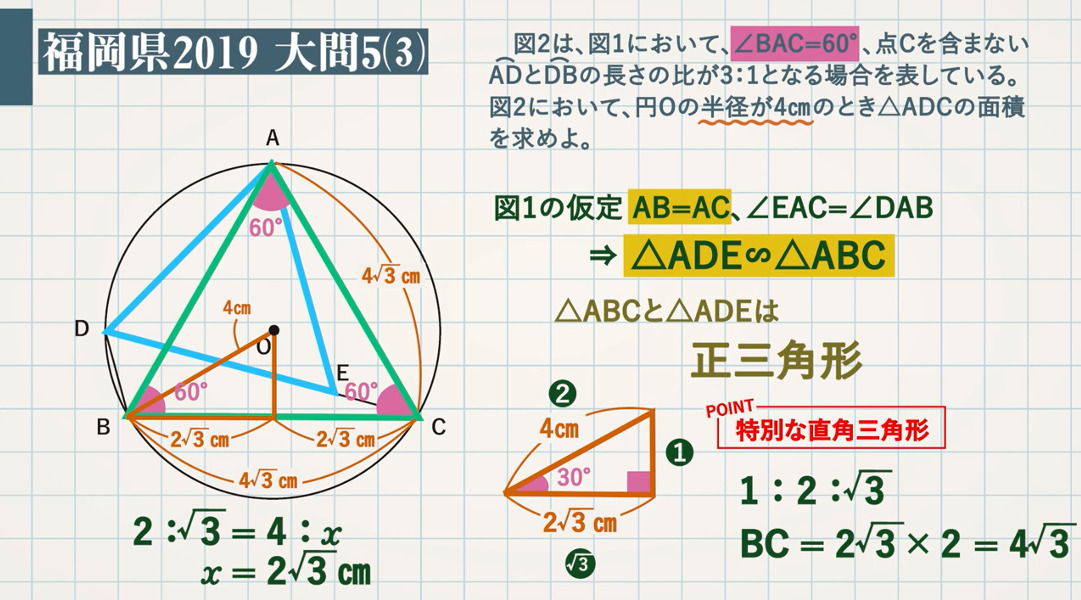



円周角 相似 三平方 特別な直角三角形の比を使い面積を求める 教遊者
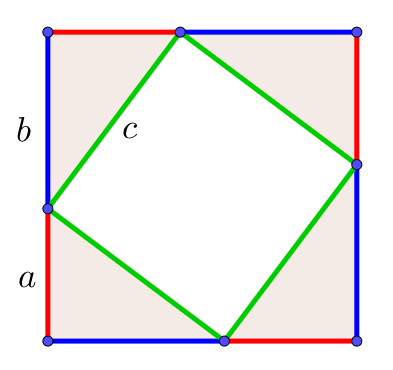



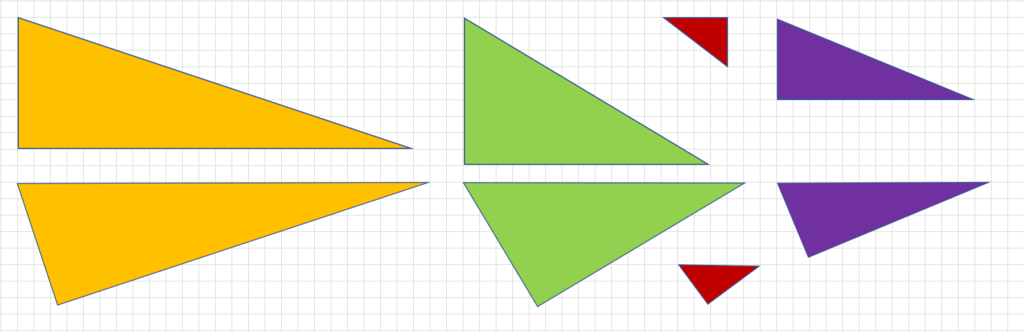
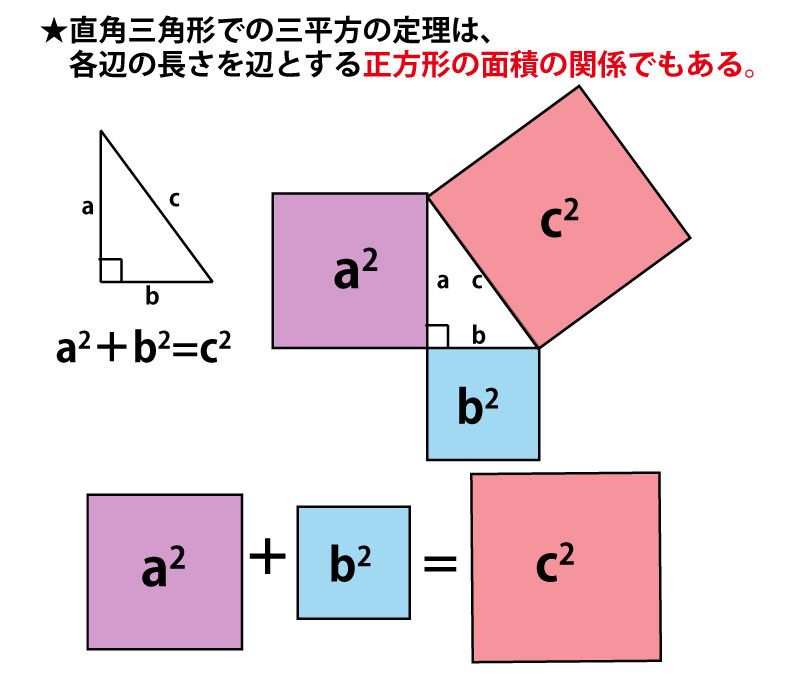
三平方の定理の証明2 4つ直角三角形と真ん中の四角 キソカラ




3 4 5の三角形で 本当に直角ができる Note Board




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




โน ตของ 中学数学 三平方の定理のキホン ช น Junior Clear




三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ




三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ



15年前期 千葉県公立高校入試 数学 第2問 5 作図 解答 解説 船橋市議会議員 朝倉幹晴公式サイト
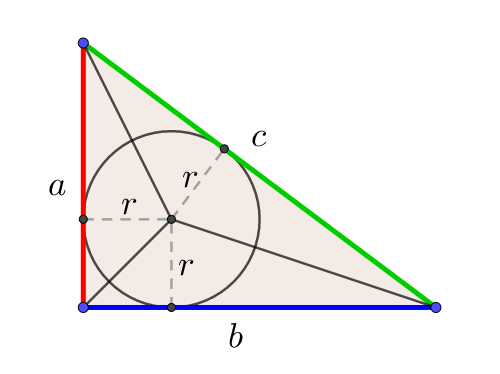



三平方の定理の証明4 直角三角形と内接円 キソカラ




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト




中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく




三平方の定理の証明 外接円と直角二等辺三角形を利用した証明 Fukusukeの数学めも
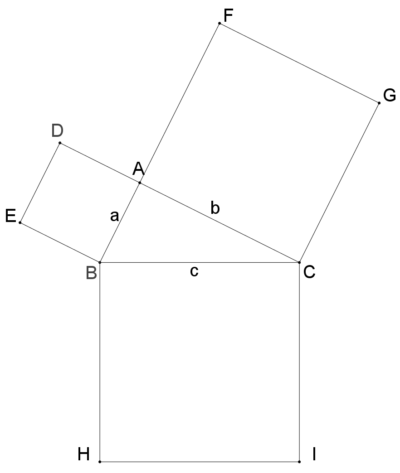



三平方の定理の証明 ユークリッドの証明 Fukusukeの数学めも




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生
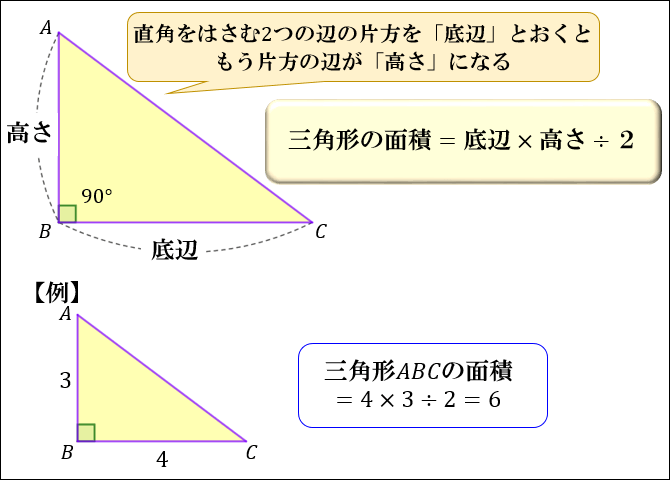



直角三角形の辺の長さ 合同条件 面積について アタリマエ




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス



3




直角三角形の辺の長さ 合同条件 面積について アタリマエ




必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集



1




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく




三平方の定理 特別な直角三角形の3辺の比 中学生からの勉強質問 数学 進研ゼミ中学講座




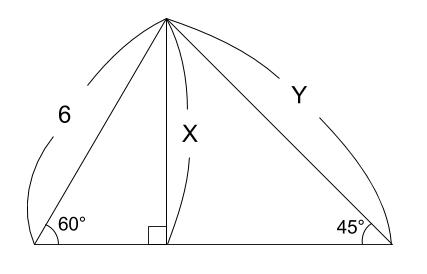
Mathematics 三平方の定理 2 特別な直角三角形 働きアリ




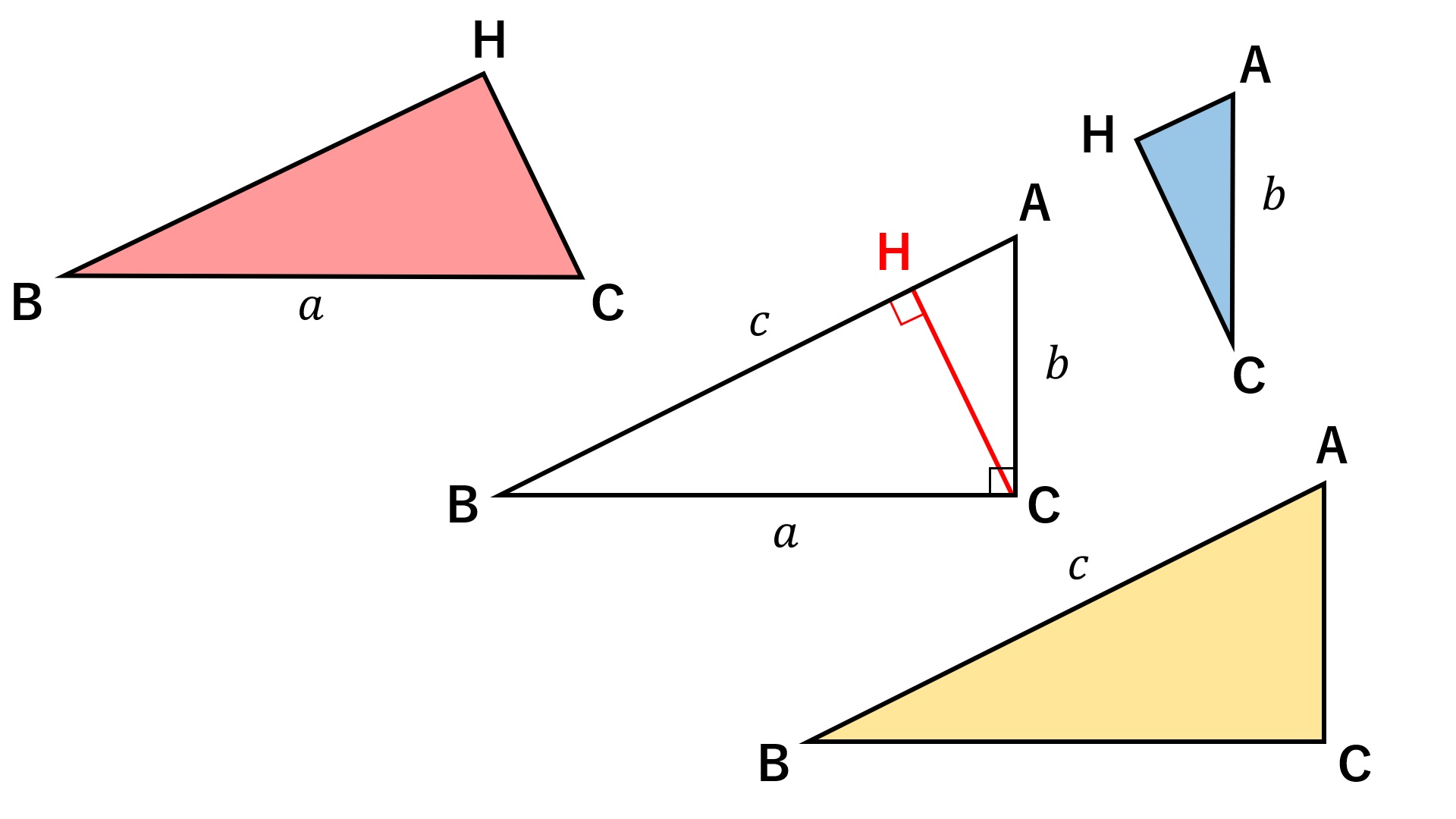
三平方の定理について考える5 直角三角形の合同条件のひとつ 身勝手な主張


